Amanatides and Woo's fast Voxel Traversal

Introduction

In this article we will dive deep into Amanatides and Woo's fast voxel traversal algorithm.
Designed for, however not limited to, ray tracing voxel grids.

Most visual examples in this article will be 2D for convenience however, the concepts are the same for 3D.
All code snippets provided will be using C++ 20 and will be for 3D voxel traversal.

You may wonder "What can voxel ray tracing do?".
Here's two screenshots taken from my own CPU voxel ray tracer:

Ray traced voxels with lighting.

Ray traced voxel terrain.

Together we're going to find out how and why this algorithm works.
So, let's dive in!

Prerequisites

To get started tracing anything, we need some data to traverse!
Let's setup a little VoxelTracer class together:

constexpr int GRID_SIDE = 32;

class VoxelTracer {
    /* Grid voxel data. */
    unsigned int grid[GRID_SIDE * GRID_SIDE * GRID_SIDE];

    /* Grid minimum and maximum point in world space. (x, y, z) */
    vec3 grid_min, grid_max;

  public:
    VoxelTracer() { 
        grid_min = vec3(0, 0, 0);
        grid_max = vec3(1, 1, 1);

        /* TODO: fill `grid` with data */
    }

    /**
     * @brief Find the nearest intersection with the grid.
     * @param ro Ray origin
     * @param rd Ray direction (normalized)
     * @return `1e30f` if no intersection was found.
     */
    float find_nearest(const vec3& ro, const vec3& rd) const;
};

What to fill grid with is up to you.
Each voxel in the grid is stored as a color unsigned int, RGBA.

For some inspiration: you could fill it with a noise pattern, like Perlin noise.

Futhermore, before we start the traversal we need to intersect our ray with the grid bounding box.
If our ray doesn't intersect the grid then we don't need to traverse it.
If our ray does intersect we will also get the time along the ray where it enters the grid called entry_t.

/**
 * @brief Ray vs AABB intersection test. (can be optimized further)
 * @param ro Ray origin
 * @param rd Ray direction (normalized)
 * @return Ray entry time, `1e30f` if no intersection was found.
 */
float ray_aabb(const vec3& min, const vec3& max, const vec3& ro, const vec3& rd) {
    float tmin = 0, tmax = 1e30f;

    /* Loop will be unrolled */
    for (int axis = 0; axis < 3; ++axis) {
        const float t1 = (min[axis] - ro[axis]) / rd[axis];
        const float t2 = (max[axis] - ro[axis]) / rd[axis];

        const float dmin = min(t1, t2);
        const float dmax = max(t1, t2);

        tmin = max(dmin, tmin);
        tmax = min(dmax, tmax);
    }

    if (tmax >= tmin) return tmin;
    return 1e30f; /* miss */
}

^{Snippet A.}

Snippet A shows a basic ray vs aabb intersection test you can use.
It is not an optimal one, nevertheless it will get the job done for now.

We can now put this intersection test at the top of our find_nearest function.
And for now, we can just return entry_t if there was a hit.

float VoxelTracer::find_nearest(const vec3& ro, const vec3& rd) const {
    /* Find the ray entry point */ 
    const float entry_t = ray_aabb(grid_min, grid_max, ro, rd);

    if (entry_t == 1e30f) return 1e30f; /* miss */

    /* TODO: voxel traversal */

    return entry_t; /* hit */
}

If we shoot a ray for each pixel on screen, and turn the output of find_nearest into a grayscale color.
We should get something that looks like this:

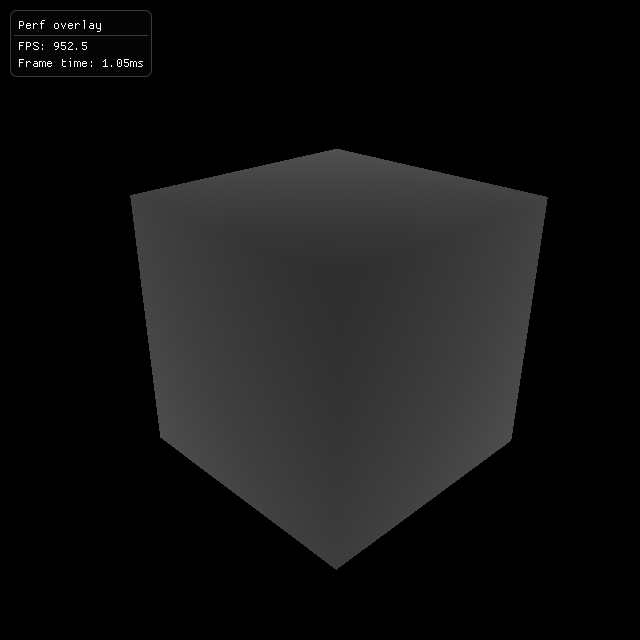Depth output of our ray / AABB intersection test.

Traversal Concept

The concept of Amanatides and Woo's algorithm is simple:
We find at what time along the ray each axis crosses its next cell boundary.
The maximum time until we cross the next axis cell boundary is often called tmax.

At any point in the grid our next step will be on the axis where tmax is the smallest.
That might sound confusing, to hopefully make it more clear, I made this graphic:

We can see that on the 1st step, tmax.x is the smallest, because the x axis will cross its cell boundary before the y axis.
Then on the 2nd step, tmax.x was updated and it is now larger than tmax.y, therefore the next step is on the y axis.

Now the question is "How do we calculate tmax?".
That's what we're going to find out next.

Traversal Setup

Now that we have our VoxelTracer, and we understand the basic concept, we can start implementing the algorithm.
Let's start with 2 important variables which will remain constant during traversal:

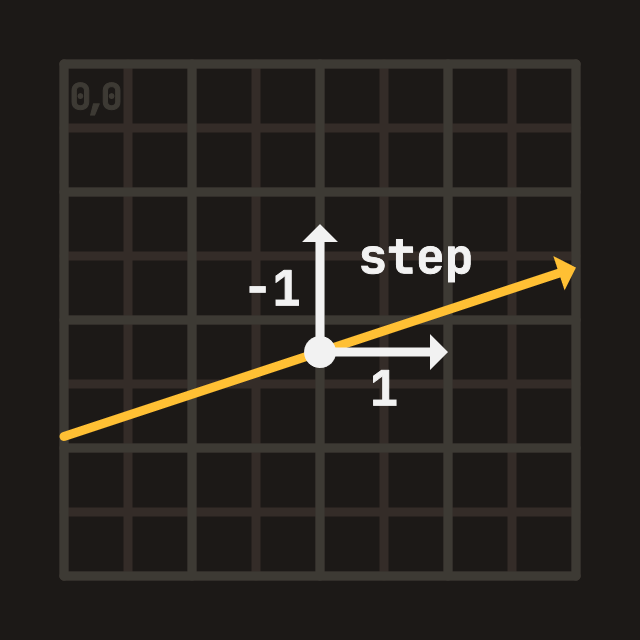Figure B: Step (direction signs)

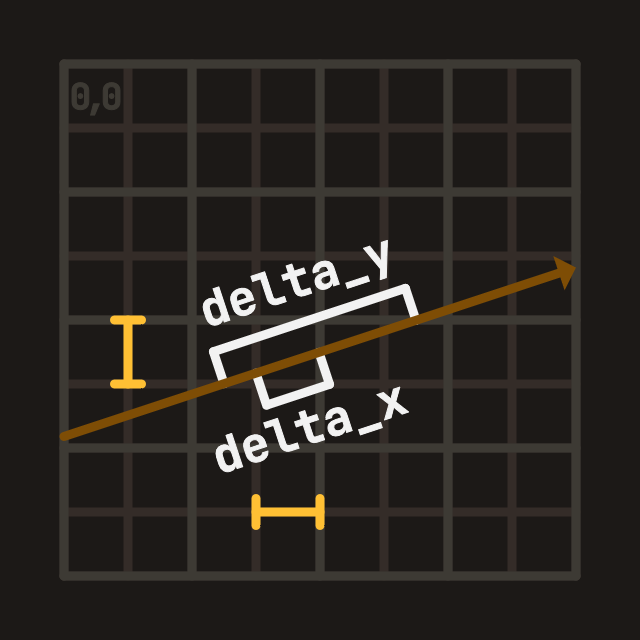Figure C: Delta (reciprocal direction)

The first variable step will be used to move through the grid along the ray direction.
Computed for each axis, if the ray direction axis is positive it is 1 and -1 if negative.
Here's what that would look like in C++:

/** @brief Get the sign of a float (-1 or 1) */
inline int getsign(const float f) { return 1 - (int)(((unsigned int&)f) >> 31) * 2; }

/** @brief Get the signs of a 3D vector (-1 or 1) */
inline vec3 sign_of_dir(const vec3& v) {
    return vec3(getsign(v.x), getsign(v.y), getsign(v.z));
}

The second variable we need is delta, it is used to update tmax during traversal.
Computed for each axis, it is the absolute of 1.0 divided by the ray direction axis, also referred to as the reciprocal.

Now there's just 2 more variables left, these variables will be updated every step during traversal.

Figure D: Finding entry cell by truncating

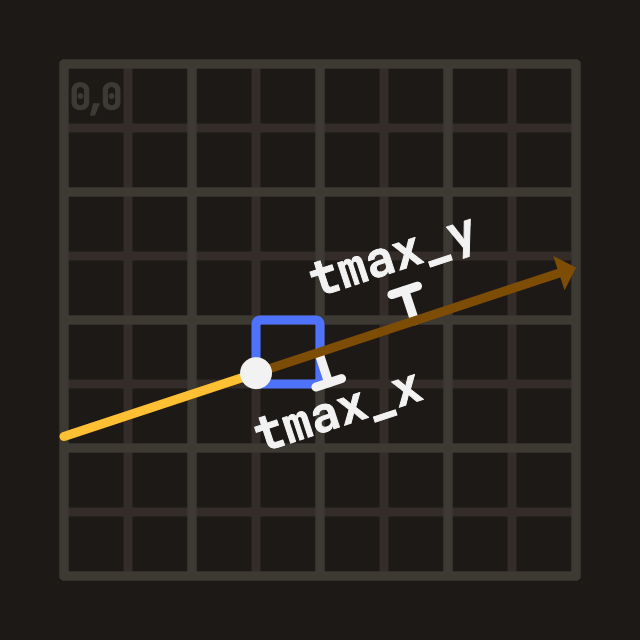Figure E: Time at next cell boundary (tmax)

The third variable is our pos within the grid, we need to initialize it to our entry point in the grid.
This is very easy to do, we simply make sure our entry point is in grid space (1 unit = 1 grid cell)
And then we truncate the floating entry point to get our entry grid position as seen in Figure D.

It's also important to clamp the pos within the grid just in case.

Now for the last variable we need the mysterious tmax which will let us correctly determine the next step.
To initialize it, we get the offset between the grid pos and the entry point,
add only the positive part of our step, and finally divide by the ray direction rd.

/* Compute how many voxels occupy a unit in world space */
const vec3 voxels_per_unit = GRID_SIDE / (grid_max - grid_min);

/* Get the floating grid entry position */
/* `0.0001f` is to slightly nudge the point inside the grid */
const vec3 entry_pos = ((ro + rd * (entry_t + 0.0001f)) - grid_min) * voxels_per_unit;

/* Initialize the time along the ray when each axis crosses its next cell boundary */
vec3 tmax = (pos - entry_pos + max(step, 0)) / rd;

Adding only the positive part of our step is important because each grid cells origin lies in its top left.
So when our ray is moving in the positive direction, we need to adjust for that fact,
while in the negative direction it is already correct.

Dividing by the ray direction is done to transform our tmax into the "ray direction space".
This is important because later we will be updating tmax using our delta.

Finally! We have everything setup, and we're ready to start traversing!

Traversal

Now that everything is already setup for us, we get to the easiest part, the actual traversal.
As I mentioned in the Concept part of the article, we will simply step based on the smallest axis of tmax.
And after every step, we update our pos and tmax.

int axis = 0;
for (...) {
    /* Fetch the cell at our current position */
    const int i = pos.z * GRID_SIDE * GRID_SIDE + pos.y * GRID_SIDE + pos.x;
    const unsigned int voxel = grid[i];

    /* Check if we hit a voxel which isn't 0 */
    if (voxel) {
        if (steps == 0) return entry_t;

        /* Return the time of intersection! */
        return entry_t + (tmax[axis] - delta[axis]) / voxels_per_unit[axis];
    }

    /* Step on the axis where `tmax` is the smallest */
    if (tmax.x < tmax.y) {
        if (tmax.x < tmax.z) {
            pos.x += step.x;
            if (pos.x < 0 || pos.x >= GRID_SIDE) break;
            axis = 0;
            tmax.x += delta.x;
        } else {
            pos.z += step.z;
            if (pos.z < 0 || pos.z >= GRID_SIDE) break;
            axis = 2;
            tmax.z += delta.z;
        }
    } else {
        if (tmax.y < tmax.z) {
            pos.y += step.y;
            if (pos.y < 0 || pos.y >= GRID_SIDE) break;
            axis = 1;
            tmax.y += delta.y;
        } else {
            pos.z += step.z;
            if (pos.z < 0 || pos.z >= GRID_SIDE) break;
            axis = 2;
            tmax.z += delta.z;
        }
    }
}

^{Snippet B.}

In Snippet B, we also track axis, the previous axis we stepped on.
Because when we hit something, we want to return the time of intersection with whatever we hit.
Which is the previous tmax along the previously stepped axis.
We can go back one step by subtracting delta[axis] from tmax[axis]:

entry_t + (tmax[axis] - delta[axis]) / voxels_per_unit[axis]

Except if steps == 0 that means we hit a voxel on the edge of the grid, so we just return entry_t instead.

And that's it, that's the entire algorithm implemented and ready to go!

All Together Now!

Now with everything put together, the final find_nearest function looks like this:

constexpr int MAX_STEPS = 128;

float VoxelTracer::find_nearest(const vec3& ro, const vec3& rd) const { 
    /* Find the ray entry point */ 
    const float entry_t = ray_aabb(grid_min, grid_max, ro, rd);

    if (entry_t == 1e30f) return 1e30f; /* miss */

    /* Compute how many voxels occupy a unit in world space */
    const vec3 voxels_per_unit = GRID_SIDE / (grid_max - grid_min);

    /* Get the floating grid entry position */
    /* `0.0001f` is to slightly nudge the point inside the grid */
    const vec3 entry_pos = ((ro + rd * (entry_t + 0.0001f)) - grid_min) * voxels_per_unit;

    /* Get our traversal constants */
    const vec3 step = sign_of_dir(rd);
    const vec3 delta = fabs(1.0f / rd);

    /* IMPORTANT: Safety clamp the entry point inside the grid */
    vec3 pos = clamp(floor(entry_pos), 0, GRID_SIDE);

    /* Initialize the time along the ray when each axis crosses its next cell boundary */
    vec3 tmax = (pos - entry_pos + max(step, 0)) / rd;

    /* The traversal loop */
    int axis = 0;
    for (int steps = 0; steps < MAX_STEPS; ++steps) {
        /* Fetch the cell at our current position */
        const int i = pos.z * GRID_SIDE * GRID_SIDE + pos.y * GRID_SIDE + pos.x;
        const unsigned int voxel = grid[i];

        /* Check if we hit a voxel which isn't 0 */
        if (voxel) {
            if (steps == 0) return entry_t;

            /* Return the time of intersection! */
            return entry_t + (tmax[axis] - delta[axis]) / voxels_per_unit[axis];
        }

        /* Step on the axis where `tmax` is the smallest */
        if (tmax.x < tmax.y) {
            if (tmax.x < tmax.z) {
                pos.x += step.x;
                if (pos.x < 0 || pos.x >= GRID_SIDE) break;
                axis = 0;
                tmax.x += delta.x;
            } else {
                pos.z += step.z;
                if (pos.z < 0 || pos.z >= GRID_SIDE) break;
                axis = 2;
                tmax.z += delta.z;
            }
        } else {
            if (tmax.y < tmax.z) {
                pos.y += step.y;
                if (pos.y < 0 || pos.y >= GRID_SIDE) break;
                axis = 1;
                tmax.y += delta.y;
            } else {
                pos.z += step.z;
                if (pos.z < 0 || pos.z >= GRID_SIDE) break;
                axis = 2;
                tmax.z += delta.z;
            }
        }
    }

    return 1e30f; /* miss */
}

And when we once again shoot a ray for each pixel into the scene.
We get to finally see some voxels on screen!

Voxel ray tracing in action!

Wrapping Up

Thank you for reading all the way to the end, I hope you now have a better understanding of the algorithm.
And I hope you enjoyed reading this article.

If you have anymore questions, or you found something incorrect in the article, let me know on Twitter (X).
Also feel free to send me pictures of your voxel traversal working! :)